Комплексные числа - математика и искусство
Главное меню:
Комплексные числа
Комплексные или мнимые числа впервые появились в известном сочинении Кардано «Великое искусство, или об алгебраических правилах» 1545 года. По мнению автора, эти числа не были пригодны к употреблению. Однако это утверждение было позднее опровергнуто. В частности, Бомбелли в 1572 году при решении кубического уравнения обосновал пользу мнимых чисел. Он составил основные правила действий с комплексными числами. И все же долгое время в математическом мире не было единого представления о сущности комплексных чисел.
Впервые символ мнимых чисел был предложен выдающимся математиком Эйлером. Предложенная символика выглядела следующим образом: i = sqr -1, где i — imaginarius, что означает фиктивный.
Необходимость в числах нового типа появилась при решении квадратных уравнений для случая D < 0 (где D — дискриминант квадратного уравнения). В настоящее время комплексные числа нашли широкое применение в физике и технике, гидро- и аэродинамике, теории упругости и т.п.
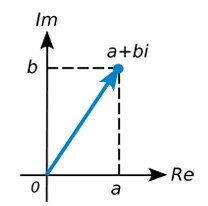
Графическая запись комплексных чисел имеет вид: a + bi, где a и b — действительные числа, а i — мнимая единица, т.e. i2 = -1. Число a называется абсциссой, a b — ординатой комплексного числа a + bi. Два комплексных числа a + bi и a — bi называются сопряжёнными комплексными числами.
• действительное число а может быть записано в форме комплексного числа: a+ 0 i или a — 0 i. К примеру, 5 + 0 i и 5 — 0 i означают одно и то же число 5.
• комплексное число 0+ bi называется чисто мнимым числом. Запись bi означает то же самое, что и 0+ bi.
• два комплексных числа a + bi и c + di считаются равными, если a = c и b = d.
К основным действиям над комплексными числами относятся:
• Сложение. Комплексное число ( a + c ) + ( b + d ) i называется суммой комплексных чисел a + bi и c + di. Следовательно, при сложении комплексных чисел отдельно складываются их абсциссы и ординаты.
• Вычитание. Комплексное число ( a — c ) + ( b — d ) i называется разностью двух комплексных чисел a + bi (уменьшаемое) и c + di (вычитаемое). Отсюда следует, что при вычитании двух комплексных чисел отдельно вычитаются их абсциссы и ординаты.
• Умножение. Произведением комплексных чисел a + bi и c + di является комплексное число ( ac — bd ) + ( ad + bc ) i. Это определение справедливо при соблюдении двух требований:
1. числа a + bi и c + di должны перемножаться, как алгебраические двучлены
2. число i обладает основным свойством: i^2 = -1.
К примеру, (a + bi)(a — bi) = a^2 + b^2. Отсюда следует, что произведение двух сопряжённых комплексных чисел равно действительному положительному числу.
• Деление. Разделить комплексное число a + bi (делимое) на другое c + di (делитель) — значит отыскать третье число e + f i (частное), умножение которого на делитель c + di даёт в результате делимое a + bi. Деление возможно только в случае, если делитель не равен нулю.
В геометрическом представлении комплексные числа в отличие от действительных, которые изображаются на числовой прямой точками, отмечаются точками на координатной плоскости. Возьмем для этого прямоугольные (декартовы) координаты с одинаковыми масштабами на осях. В этом случае комплексное число a + bi будет представлено точкой Р с абсциссой а и ординатой b. Такая система координат называется комплексной плоскостью.
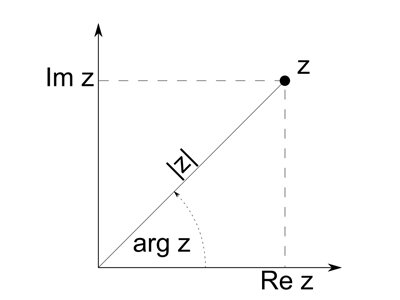
Модулем комплексного числа является длина вектора OP, изображающего комплексное число комплексной плоскости. Модуль комплексного числа a + bi записывается в виде |a + bi| или буквой r и равен:
r = |a + ib| = sqr a2 + b2.
У сопряженных комплексных чисел имеется одинаковый модуль.
Аргументом комплексного числа является угол φ между осью OX и вектором OP, изображающим комплексное число. Отсюда получаем, tan φ = b/a.
Тригонометрическая форма комплексного числа выражается через модуль r и аргумент φ абсциссы a и ординаты b комплексного числа a + bi.
a = r cosφ, b = r sinφ.
a + bi = r ( cosφ + i sinφ).
/БДЭ Математика/