Розы Гранди - математика и искусство
Главное меню:
- Кривые
- Розы Гранди
- Астроида
- Гипоциклоида
- Декартов лист
- Кардиоида
- Квадратиса
- Конхоида Никомеда
- Крест
- Лемниската
- Спирали
- Локон Аньези
- Овалы Кассини
- Парабола Нейля
- Строфоида
- Трисектриса Маклорена
- Трохоида
- Улитка Паскаля
- Цепная линия
- Циссоида Диоклеса
- Циклоида
- Эвольвента
- Эпициклоида
- Красивые кривые
- Кривые Лиссажу
- Линейчатые поверхности
Розы Гранди
Математический цветник
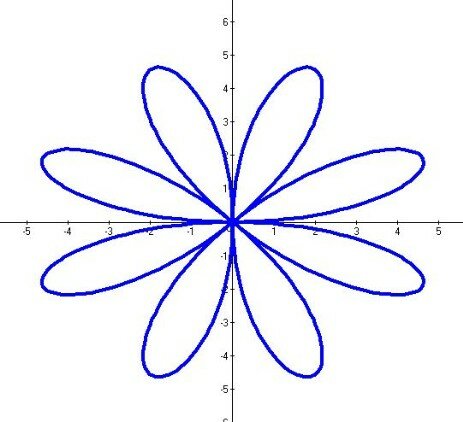
Как-то раз итальянский геометр Гвидо Гранди(1671-1742) создал розы. Розы радуют глаз правильными и плавными линиями, но их очертания не каприз природы - они предопределены специально подобранными математическими зависимостями. Семейство роз Гранди описывается уравнением в полярных координатах г=a sinк , где а и к - некоторые постоянные.
При к нечётном роза состоит из к лепестков, при m чётном — из 2к лепестков; при к рациональном лепестки частично покрывают друг друга. При иррациональном K роза имеет бесконечное число лепестков.
В уравнении r=asin(bk) значение a отвечает за длину лепестков, а значения b – за количество и форму.
Очарованный результатами Гранди, немецкий геометр, математик-натуралист XIX в. Б. Хабенихт также решил заняться математическим «растениеводством». Полагая, что абрис (очертание) листа или цветочного лепестка в полярных координатах описывается выражением r=f(ϕ), где f(ϕ) для каждого отдельного растения представляет определённую комбинацию тригонометрических функций, Хабенихт путём многочисленных экспериментов «вырастил» замечательные экспонаты.
Хабенихт в своих работах приводит ряд полученных им уравнений, которые с хорошим приближением аналитически выражают очертания различных листьев и плодов. Он также рассматривает контур листа как замкнутую кривую, которая в полярной системе координат имеет уравнение.
Если предположить, что кривая, изображающая контур листа, симметрична относительно полярной оси, а функция является конечной суммой, то эта сумма должна состоять из косинусов или синусов. Исходя из этого общего уравнения, Хабенихт исследует его частные случаи. Постепенно усложняя уравнение он получает большое количество уравнений контуров листьев: плюща, крапивы, листьев кислицы и др.



 Полярная система координат — двухмерная система координат, в которой каждая точка на плоскости определяется двумя числами — полярным углом и полярным радиусом. Полярная система координат особенно полезна в случаях, когда отношения между точками проще изобразить в виде радиусов и углов; в более распространённой, декартовой или прямоугольной системе координат, такие отношения можно установить только путём применения тригонометрических уравнений.
Полярная система координат — двухмерная система координат, в которой каждая точка на плоскости определяется двумя числами — полярным углом и полярным радиусом. Полярная система координат особенно полезна в случаях, когда отношения между точками проще изобразить в виде радиусов и углов; в более распространённой, декартовой или прямоугольной системе координат, такие отношения можно установить только путём применения тригонометрических уравнений.
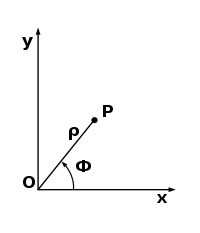
Полярная система координат задаётся лучом, который называют нулевым или полярной осью. Точка, из которой выходит этот луч, называется началом координат или полюсом. Любая точка на плоскости определяется двумя полярными координатами: радиальной и угловой. Радиальная координата (обычно обозначается ϕ соответствует расстоянию от точки до начала координат. Угловая координата, также называется полярным углом или азимутом и обозначается , равна углу, на который нужно повернуть против часовой стрелки полярную ось для того, чтобы попасть в эту точку.
Определённая таким образом радиальная координата может принимать значения от нуля до бесконечности, а угловая координата изменяется в пределах от 0° до 360°. Однако, для удобства область значений полярной координаты можно расширить за пределы полного угла, а также разрешить ей принимать отрицательные значения, что отвечает повороту полярной оси по часовой стрелке.
розы Гранди видео, а также здесь
